Volta e meia eu vejo em algumas redes algumas pessoas desenvolvedoras falando sobre, use isso, não use tal, e dizendo que devs juniors já deviam saber disso ou daquilo, porém normalmente isso tem relação a funções extendidas de javascript, python, etc.. mas poucos se atentam a uma questão que pode ser bem crítica, que é a complexidade do código gerado usando essas funções, e nesse artigo gostaria apenas de mostrar exemplos do que são e de pequenas implementações de algoritmos e diversos momentos de complexidade, a notação usada será a Big O
Espero que gostem 🙂
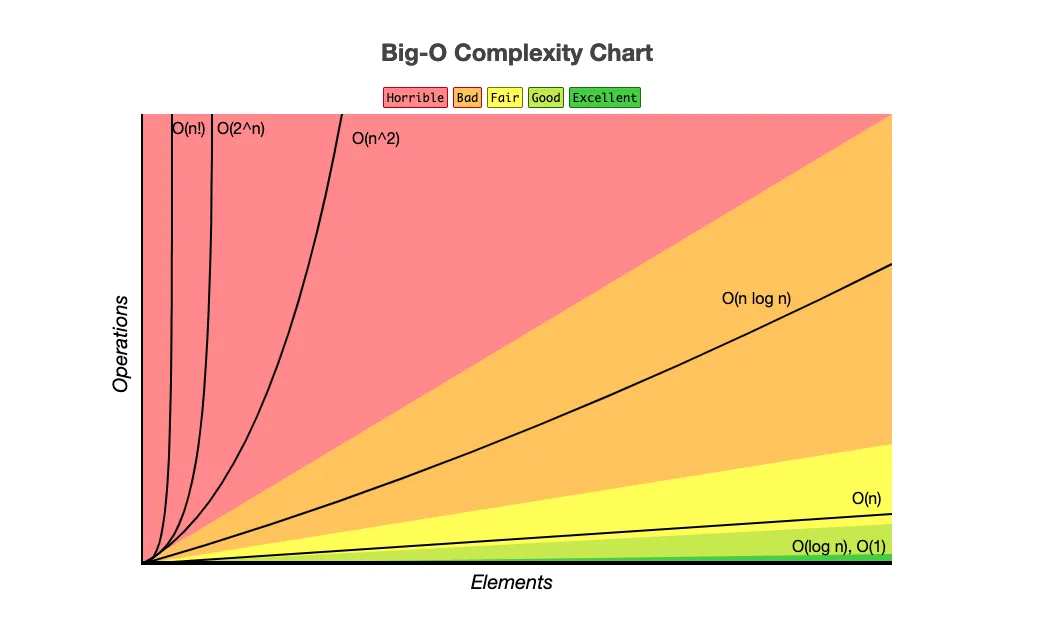
Primeiramente, o que é Big O?
Na ciência da computação, a notação Big O é uma notação matemática que descreve o comportamento limitante de uma função quando o argumento tende a um valor específico ou ao infinito. É membro de uma família maior de notações conhecida como notação Landau, notação Bachmann–Landau, ou notação assintótica.
A notação Big O é usada para classificar algoritmos de acordo com seu tempo de execução ou requisitos de espaço, conforme a entrada de dados aumenta.
Em termos simples, a notação Big O diz o quanto o tempo de execução ou os requisitos de espaço de um algoritmo aumentam conforme o tamanho da entrada aumenta.
Por exemplo, um algoritmo de complexidade O(n) é um algoritmo cujo tempo de execução é proporcional ao tamanho da entrada. Isso significa que, se o tamanho da entrada dobrar, o tempo de execução do algoritmo também dobrará.
Aqui estão alguns exemplos de notação Big O:
- O(1): Constante
- O(log n): Logarítmico
- O(n): Linear
- O(n log n): Quasilinear
- O(n²): Quadrático
- O(2^n): Exponencial
- O(n!): Fatorial
A notação Big O é uma ferramenta importante para a análise de algoritmos. Ela ajuda a identificar algoritmos eficientes e a otimizar algoritmos ineficientes.
Aqui estão alguns exemplos de como a notação Big O pode ser usada:
- Um programador pode usar a notação Big O para comparar dois algoritmos diferentes e escolher o algoritmo mais eficiente.
- Um analista de desempenho pode usar a notação Big O para estimar o tempo de execução de um algoritmo para uma entrada de tamanho específico.
- Um engenheiro de software pode usar a notação Big O para identificar gargalos de desempenho em um sistema.
A notação Big O é uma ferramenta poderosa que pode ser usada para melhorar o desempenho de software.
Sabendo disso vamos começar a listar alguns exemplos
Vamos do mais simples aos mais complexos
O(1): Constante
Um exemplo de algoritmo de complexidade O(1) é o algoritmo max(), que retorna o maior valor de dois números. Este algoritmo não depende do tamanho da entrada, pois sempre executa as mesmas instruções, independentemente do tamanho dos números.
function max(a, b) {
return a > b ? a : b;
}Outro exemplo é o algoritmo String.length(), que retorna o comprimento de uma string. Este algoritmo também não depende do tamanho da entrada, pois sempre executa as mesmas instruções, independentemente do tamanho da string.
const string = "Hello, world!";
const length = string.length;Um exemplo clássico de algoritmo com complexidade O(1) é o acesso direto a um elemento em um array ou a obtenção de um valor em um objeto, já que essas operações não dependem do tamanho do conjunto de dados. Vamos ver um exemplo simples:
// Acesso direto a um elemento em um array
const array = [10, 20, 30, 40, 50];
const primeiroElemento = array[0];
console.log(primeiroElemento); // Saída: 10
// Acesso direto a um valor em um objeto
const objeto = { chave1: 'valor1', chave2: 'valor2', chave3: 'valor3' };
const valorChave2 = objeto.chave2;
console.log(valorChave2); // Saída: 'valor2'Nesses exemplos, o acesso direto ao primeiro elemento do array ou ao valor associado à chave chave2 no objeto é feito em tempo constante, independentemente do tamanho do array ou do objeto.
Em geral, algoritmos de complexidade O(1) são aqueles que não dependem do tamanho da entrada. Isso significa que eles são executados no mesmo tempo, independentemente do tamanho do problema que estão resolvendo.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(1):
Math.abs()Math.floor()Math.ceil()Math.round()Boolean.toString()Number.toString()String.fromCharCode()
Algoritmos de complexidade O(1) são geralmente os mais eficientes, pois são executados no mesmo tempo, independentemente do tamanho do problema que estão resolvendo.
O(log n): Logarítmico
Um exemplo comum de algoritmo com complexidade O(log n) é a busca binária em um array ordenado. Nesse caso, a complexidade logarítmica é possível porque a cada iteração, a quantidade de dados a serem processados é reduzida pela metade.
function buscaBinaria(array, alvo) {
let inicio = 0;
let fim = array.length - 1;
while (inicio <= fim) {
const meio = Math.floor((inicio + fim) / 2);
if (array[meio] === alvo) {
return meio; // Retorna o índice se o elemento for encontrado
} else if (array[meio] < alvo) {
inicio = meio + 1;
} else {
fim = meio - 1;
}
}
return -1; // Retorna -1 se o elemento não for encontrado
}
const meuArrayOrdenado = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const resultadoBuscaBinaria = buscaBinaria(meuArrayOrdenado, 7);
if (resultadoBuscaBinaria !== -1) {
console.log(`Elemento encontrado no índice ${resultadoBuscaBinaria}`);
} else {
console.log('Elemento não encontrado no array');
}
Neste exemplo, a função buscaBinaria realiza uma busca eficiente em um array ordenado. Ela divide repetidamente o array ao meio até que o elemento seja encontrado ou a busca não possa mais ser dividida. A cada iteração, a quantidade de dados a serem processados é reduzida pela metade, resultando em uma complexidade de tempo O(log n), onde n é o número de elementos no array.
A busca binária é eficiente para conjuntos de dados ordenados, especialmente quando o conjunto de dados é grande, pois reduz significativamente o número de iterações necessárias para encontrar um elemento.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(log n):
Array.indexOf()Array.lastIndexOf()Tree.find()Tree.contains()Set.has()Map.get()
Algoritmos de complexidade O(log n) são geralmente muito eficientes, mesmo para problemas grandes.
O(n): Linear
Um exemplo de algoritmo de complexidade O(n) é o algoritmo forEach(), que executa uma função callback para cada elemento de um array. Este algoritmo precisa iterar por cada elemento do array, portanto, seu tempo de execução é proporcional ao tamanho do array.
const array = [1, 2, 3, 4, 5];
array.forEach((element) => {
console.log(element);
});Outro exemplo é o algoritmo for(), que também itera por cada elemento de um array.
const array = [1, 2, 3, 4, 5];
for (const element of array) {
console.log(element);
}Outro exemplo comum de algoritmo com complexidade O(n) é o algoritmo de busca linear em um array não ordenado. Nesse caso, a complexidade é linear, pois o número de operações aumenta linearmente com o tamanho do array.
function buscaLinear(array, alvo) {
for (let i = 0; i < array.length; i++) {
if (array[i] === alvo) {
return i; // Retorna o índice se o elemento for encontrado
}
}
return -1; // Retorna -1 se o elemento não for encontrado
}
const meuArray = [3, 7, 1, 4, 2, 8, 5];
const resultado = buscaLinear(meuArray, 4);
if (resultado !== -1) {
console.log(`Elemento encontrado no índice ${resultado}`);
} else {
console.log('Elemento não encontrado no array');
}Neste exemplo, a função buscaLinear percorre cada elemento do array até encontrar o elemento desejado ou até percorrer todo o array. Se o elemento for encontrado, a função retorna o índice desse elemento; caso contrário, retorna -1. O número de iterações é proporcional ao tamanho do array, resultando em uma complexidade de O(n), onde n é o número de elementos no array.
Em geral, algoritmos de complexidade O(n) são aqueles que precisam iterar por cada elemento de uma entrada. Isso significa que seu tempo de execução é proporcional ao tamanho da entrada.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(n):
Array.map()Array.filter()Array.reduce()Array.find()Array.some()Array.every()
Algoritmos de complexidade O(n) são geralmente eficientes, mas podem se tornar ineficientes para problemas grandes.
O(n log n): Quasilinear
Um exemplo comum de algoritmo com complexidade O(n log n) é o algoritmo de ordenação Merge Sort. Este algoritmo divide recursivamente a lista pela metade, ordena cada metade e, em seguida, combina as metades ordenadas. A complexidade de tempo do Merge Sort é O(n log n).
function mergeSort(array) {
if (array.length <= 1) {
return array;
}
const meio = Math.floor(array.length / 2);
const metadeEsquerda = array.slice(0, meio);
const metadeDireita = array.slice(meio);
return merge(mergeSort(metadeEsquerda), mergeSort(metadeDireita));
}
function merge(arr1, arr2) {
let resultado = [];
let i = 0;
let j = 0;
while (i < arr1.length && j < arr2.length) {
if (arr1[i] < arr2[j]) {
resultado.push(arr1[i]);
i++;
} else {
resultado.push(arr2[j]);
j++;
}
}
return resultado.concat(arr1.slice(i)).concat(arr2.slice(j));
}
const meuArrayDesordenado = [6, 2, 8, 3, 1, 9, 7, 5, 4];
const arrayOrdenado = mergeSort(meuArrayDesordenado);
console.log("Array desordenado:", meuArrayDesordenado);
console.log("Array ordenado:", arrayOrdenado);Neste exemplo, a função mergeSort divide recursivamente o array pela metade até que cada parte seja composta por um único elemento. Em seguida, a função merge combina as partes ordenadas, mantendo a ordenação no processo. A complexidade de tempo do Merge Sort é O(n log n), onde n é o número de elementos no array. Essa complexidade faz do Merge Sort uma escolha eficiente para ordenar grandes conjuntos de dados.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(n log n):
QuickSort()HeapSort()RadixSort()BucketSort()
Algoritmos de complexidade O(n log n) são geralmente eficientes, mesmo para problemas grandes.
O(n²): Quadrático
Um exemplo de algoritmo de complexidade O(n²) é o algoritmo nestedLoops(), que percorre um array duas vezes, uma vez para cada elemento do array. Este algoritmo tem um loop externo que itera pelo array, e um loop interno que itera por cada elemento do array dentro do loop externo.
function nestedLoops(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
// ...
}
}
}O tempo de execução do algoritmo nestedLoops() é proporcional ao número de vezes que o loop interno é executado. Como o loop interno é executado n vezes para cada elemento do array, o tempo de execução do algoritmo é proporcional a n².
Um exemplo comum de algoritmo com complexidade O(n^2) é o algoritmo de ordenação Bubble Sort. Este algoritmo compara elementos adjacentes e os troca se estiverem na ordem errada. O processo é repetido até que o array esteja ordenado. A complexidade de tempo do Bubble Sort é O(n^2).
function bubbleSort(array) {
const tamanho = array.length;
for (let i = 0; i < tamanho - 1; i++) {
for (let j = 0; j < tamanho - i - 1; j++) {
// Compara elementos adjacentes
if (array[j] > array[j + 1]) {
// Troca os elementos se estiverem na ordem errada
const temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
return array;
}
const meuArrayDesordenado = [6, 2, 8, 3, 1, 9, 7, 5, 4];
const arrayOrdenado = bubbleSort(meuArrayDesordenado);
console.log("Array desordenado:", meuArrayDesordenado);
console.log("Array ordenado:", arrayOrdenado);Neste exemplo, a função bubbleSort utiliza dois loops aninhados para comparar e trocar elementos adjacentes até que o array esteja ordenado. A complexidade de tempo do Bubble Sort é O(n^2), onde n é o número de elementos no array. Esse tipo de algoritmo de ordenação é eficaz para conjuntos de dados pequenos, mas torna-se menos eficiente para conjuntos de dados maiores devido à sua complexidade quadrática. Existem algoritmos de ordenação mais eficientes, como o Merge Sort ou o Quick Sort, para conjuntos de dados maiores.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(n²):
bubbleSort()selectionSort()insertionSort()linearSearch()
Algoritmos de complexidade O(n²) são geralmente ineficientes para problemas grandes.
O(2^n): Exponencial
Um exemplo de algoritmo de complexidade O(2^n) é o algoritmo fibonacci(), que calcula o n-ésimo número de Fibonacci. Este algoritmo funciona recursivamente, calculando o (n-1)-ésimo número de Fibonacci e o (n-2)-ésimo número de Fibonacci, e depois somando os dois números.
function fibonacci(n) {
if (n === 0 || n === 1) {
return n;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}O tempo de execução do algoritmo fibonacci() é proporcional ao número de chamadas recursivas que são feitas. Como o número de chamadas recursivas é igual a 2^n, o tempo de execução do algoritmo é proporcional a 2^n.
Outro algoritmo com complexidade O(2^n) é o algoritmo de exponenciação exata (exponential algorithm). Nesse tipo de algoritmo, o tempo de execução cresce exponencialmente com o tamanho do problema. Aqui está um exemplo que calcula a potência de 2 usando uma abordagem recursiva:
function potenciaDeDoisRecursiva(n) {
if (n === 0) {
return 1;
} else {
return 2 * potenciaDeDoisRecursiva(n - 1);
}
}
const resultado = potenciaDeDoisRecursiva(5);
console.log("2 elevado a 5:", resultado);Neste exemplo, a função potenciaDeDoisRecursiva calcula 2 elevado à potência de n recursivamente, multiplicando por 2 a cada chamada. A complexidade de tempo desse algoritmo é O(2^n), pois a função é chamada exponencialmente em relação ao valor de n. Conforme n aumenta, o número de operações necessárias cresce exponencialmente, tornando-o ineficiente para valores grandes de n.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(2^n):
hanoiTowers()queens()sudoku()knights()
Algoritmos de complexidade O(2^n) são geralmente ineficientes para problemas grandes.
No entanto, vale ressaltar que a complexidade de um algoritmo é uma medida do seu pior caso. Em muitos casos, o algoritmo pode executar muito mais rápido que o seu pior caso. Por exemplo, o algoritmo fibonacci() é geralmente muito rápido para valores pequenos de n, mas pode se tornar muito lento para valores grandes de n.
O(n!): Fatorial
Um exemplo comum de algoritmo com complexidade O(n!) é o algoritmo de permutação (permute). Nesse tipo de algoritmo, o tempo de execução cresce fatorialmente com o tamanho do problema. Aqui está um exemplo em JavaScript que gera todas as permutações de uma lista:
function permutacoes(lista) {
function permutacoesAuxiliar(lista, inicio) {
if (inicio === lista.length - 1) {
console.log(lista.slice()); // Imprime a permutação atual
} else {
for (let i = inicio; i < lista.length; i++) {
[lista[inicio], lista[i]] = [lista[i], lista[inicio]]; // Troca os elementos
permutacoesAuxiliar(lista, inicio + 1);
[lista[inicio], lista[i]] = [lista[i], lista[inicio]]; // Desfaz a troca
}
}
}
permutacoesAuxiliar(lista, 0);
}
const minhaLista = [1, 2, 3];
permutacoes(minhaLista);Neste exemplo, a função permutacoes gera todas as permutações da lista utilizando uma abordagem recursiva. A função permutacoesAuxiliar é chamada recursivamente para cada posição na lista, trocando os elementos para gerar todas as permutações possíveis. A complexidade de tempo desse algoritmo é O(n!), onde n é o tamanho da lista. À medida que o tamanho da lista aumenta, o número de permutações cresce fatorialmente, tornando esse tipo de algoritmo ineficiente para listas grandes.
Aqui estão alguns outros exemplos de algoritmos de complexidade O(n!):
combinations()n-queens()n-rooks()factorial()
Algoritmos de complexidade O(n!) são geralmente ineficientes para problemas grandes.
Por exemplo, o algoritmo factorial() é geralmente muito rápido para valores pequenos de n, mas pode se tornar muito lento para valores grandes de n.
Como exemplo mais concreto, o algoritmo factorial() executa 60 operações para calcular o fatorial de 5, 120 operações para calcular o fatorial de 6, e assim por diante. Para valores grandes de n, o algoritmo pode se tornar inviável de ser executado.
Bom, era isso, espero que gostem 🙂
9